梯度下降笔记

梯度下降迭代公式

$$
\omega_{t+1} = \omega_t - \alpha \nabla f(\omega_t)
$$

• $\alpha$为学习率
• $\nabla f(\omega_t)$为梯度

通俗理解梯度下降迭代公式

• 首先可以确定的是我们的任务是找loss极小值(不是极值而是极小值)

• 对于f(x)的一阶导可以认为是f(x)随着x的增长而增长的趋势, 所以为了找极小值的x坐标必定和一阶导的反方向来找

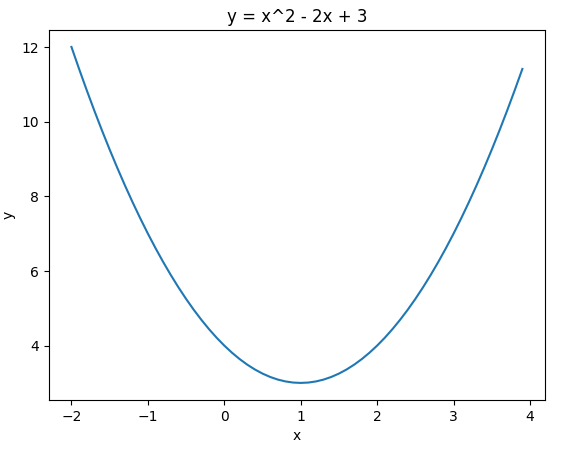
• 在此例子中, $f(x) = x^2-2x+3$, 一阶导$f’(x) = 2x -2$, 在x=2的导数为2, 可以通俗的理解为当x增长1则f(x)会增长2,
  而我们的任务是找f(x)的极小值, 所以极小值的x坐标必定是跟导数2是反方向;
  同理在x=0的导数为-2, 即x增长1则f(x)会增长-2, 极小值的x坐标方向确实和导数-2为反向

• 在这个例子中我们也可以用斜率的投影方向来理解